Pulse Train

Program Notes Provided by Viet Cuong

As I was drafting ideas for a new chamber piece and searching for a concept, my mother mentioned that my father, a former physicist, was credited in 1995 as an author of US Patent #5389931 describing radar signal processing. Reading the abstract reminded me why I chose not to pursue his path:

“A conical scan radar system (10) provides return pulses (30) to an A/D converter (38) from which a shaped pulse train is received and stored in a FIFO memory (40). The stored pulse train is then passed through first and second finite impulse response filters (42,44) for achieving sampling rate reduction prior to rendering via a programmable signal processor (64) of target detection identification and tracking.”

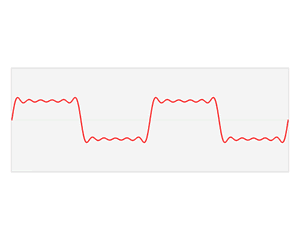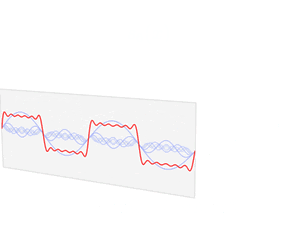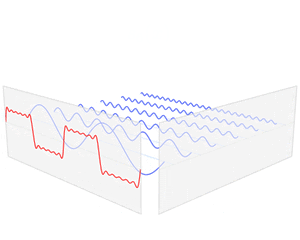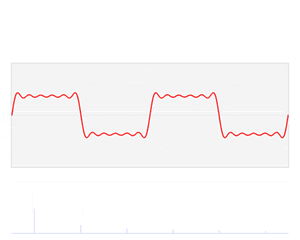
Though I had absolutely no idea what any of this meant, the phrase “pulse train” struck me as a possible title for the piece. Upon further research, I learned that a pulse train (or pulse wave) is a non sinusoidal waveform similar to a square wave, with extremely sharp changes in amplitude and contour. Because I had about three sketches that were very different texturally and harmonically, this concept fit my sketches perfectly–the jagged contour of the pulse train could provide cohesion for a piece built upon contrast within the same tempo. Therefore, shifts between disparate textures occur frequently and without warning. Ironically, it was not until after I had finished composing that I realized the piece largely has the character of a locomotive.

Explaining a Pulse Train in the Context of Music

When we hear sound, groups of waves are being created that vibrate our inner ear drum and send signals to three specific bones in our ear, called the malleus, incus, and stapes. These waves then travel to another part of our ear that moves around a liquid in the inner ear, or cochlea. This liquid then moves microscopic hairs that send electric signals to our brain, that our brain interprets as sound.

The biggest difference in the sounds we hear come from varying wavelengths that are presented to our ears. A single sound, at its most basic level, can be represented by the pushing and pulling of molecules (either through air, a liquid, or other medium). This can be graphed in the shape of a wave, and in this case a sine wave, which looks like this:

As the sound either goes up or down in pitch, the waves that we see will look either closer together, or further apart, respectively. The amount of waves per second are defined in a unit of hertz which is why we often tune an ensemble to A=440, because that particular pitch produces 440 waves per second.

All of the sounds that we hear, and particularly music, however, are not just a simple sine wave, but rather it is a fundamental sine wave (as seen here), and a series of harmonic sounds on top of this fundamental sound.

Sine waves can also represent an outlining of a circle. As shown in the graphic, each sine wave can be represented by a specific size circle that is traced as time progresses. 

When the fundamental sound is combined with its infinite level of harmonics, its sine waves are combined at the same time. Because the size of these sine waves are each unique to their own harmonic, or “pitch,” when you combine these sounds, you get what our brains interpret as a note. When all of the different sized circles are put into a single space of time, like the starting and stopping of a musical note, all of those different circles can be combined together to create a sound that is either “on” (sound can be heard) or “off” (no sound can be heard). 

As previously established, when a note is played, the fundamental of the note as well as its harmonics can all be heard at the same time. Think of this as if each frequency, whether it’s a fundamental or a harmonic, has a uniquely sized circle attributed to it. As the note is played, the fundamental fills up the space of time it is being played, and then each of the successive harmonics fills in the space that’s left (seen in the graphic here).

This added layering of smaller and smaller circles is an extremely simplified version of what is known as a Fourier Series, as can be seen in the graphic here. Each of the smaller and smaller rods, going up to infinity, represents one of the upper harmonics of an individual note. These individualized frequencies of sound, when displayed on a graph, contribute to what we now know as a square wave.

The pulse train comes from a repeated succession of sounds that are created. What Viet Cuong has done with this piece, through sudden shifts of dynamics and orchestration, is to represent a pulse train via a musical means.